(This is the third entry in The Modern Library Nonfiction Challenge, an ambitious project to read and write about the Modern Library Nonfiction books from #100 to #1. There is also The Modern Library Reading Challenge, a fiction-based counterpart to this list. Previous entry: Operating Instructions.)
 In the bustling beginnings of the twentieth century, the ferociously independent mind who forever altered the way in which we look at the universe was living in poverty.* His name was Charles Sanders Peirce and he’d anticipated Heisenberg’s uncertainty principle by a few decades. In 1892, Peirce examined what he called the doctrine of necessity, which held that every single fact of the universe was determined by law. Because before Peirce came along, there were several social scientists who were determined to find laws in everything — whether it be an explanation for why you parted your hair at a certain angle with a comb, felt disgust towards specific members of the boy band One Direction, or ran into an old friend at a restaurant one hundred miles away from where you both live. Peirce declared that absolute chance — that is, spontaneity or anything we cannot predict before an event, such as the many fish that pelted upon the heads of puzzled citizens in Shasta County, California on a January night in 1903 — is a fundamental part of the universe. He concluded that even the careful rules discovered by scientists only come about because, to paraphrase Autolycus from A Winter’s Tale, although humans are not always naturally honest, chance sometimes makes them so.
In the bustling beginnings of the twentieth century, the ferociously independent mind who forever altered the way in which we look at the universe was living in poverty.* His name was Charles Sanders Peirce and he’d anticipated Heisenberg’s uncertainty principle by a few decades. In 1892, Peirce examined what he called the doctrine of necessity, which held that every single fact of the universe was determined by law. Because before Peirce came along, there were several social scientists who were determined to find laws in everything — whether it be an explanation for why you parted your hair at a certain angle with a comb, felt disgust towards specific members of the boy band One Direction, or ran into an old friend at a restaurant one hundred miles away from where you both live. Peirce declared that absolute chance — that is, spontaneity or anything we cannot predict before an event, such as the many fish that pelted upon the heads of puzzled citizens in Shasta County, California on a January night in 1903 — is a fundamental part of the universe. He concluded that even the careful rules discovered by scientists only come about because, to paraphrase Autolycus from A Winter’s Tale, although humans are not always naturally honest, chance sometimes makes them so.
The story of how Peirce’s brave stance was summoned from the roiling industry of men with abaci and rulers is adeptly set forth in Ian Hacking’s The Taming of Chance, a pleasantly head-tingling volume that I was compelled to read twice to ken the fine particulars. It’s difficult to articulate how revolutionary this idea was at the time, especially since we now live in an epoch in which much of existence feels preordained by statistics. We have witnessed Nate Silver’s demographic models anticipate election results and, as chronicled in Moneyball, player performance analysis has shifted the way in which professional baseball teams select their roster and steer their lineup into the playoffs, adding a strange computational taint that feels as squirmy as performance enhancing drugs.
But there was a time in human history in which chance was considered a superstition of the vulgar, even as Leibniz, seeing that a number of very smart people were beginning to chatter quite a bit about probability, argued that the true measure of a Prussian state resided in how you tallied the population. Leibniz figured that if Prussia had a central statistic office, it would not only be possible to gauge the nation’s power but perhaps lead to certain laws and theories about the way these resources worked.
This was obviously an idea that appealed to chin-stroking men in power. One does not rule an empire without keeping the possibility of expansion whirling in the mind. It didn’t take long for statistics offices to open and enthusiasts to start counting heads in faraway places. (Indeed, much like the early days of computers, the opening innovations originated from amateurs and enthusiasts.) These early statisticians logged births, deaths, social status, the number of able-bodied men who might be able to take up weapons in a violent conflict, and many other categories suggested by Leibniz (and others that weren’t). And they didn’t just count in Prussia. In 1799, Sir John Sinclair published a 21 volume Statistical Account of Scotland that undoubtedly broke the backs of many of the poor working stiffs who were forced to carry these heavy tomes to the guys determined to count it all. Some of the counters became quite obsessive in their efforts. Hacking reports that Sinclair, in particular, became so sinister in his efforts to get each minister of the Church of Scotland to provide a detailed congregation schedule that he began making threats shrouded in a jocose tone. Perhaps the early counters needed wild-eyed dogged advocates like Sinclair to establish an extremely thorough baseline.
The practice of heavy-duty counting resulted, as Hacking puts it, in a bona-fide “avalanche of numbers.” Yet the intersection of politics and statistics created considerable fracas. Hacking describes the bickering and backbiting that went down in Prussia. What was a statistical office? Should we let the obsessive amateurs run it? Despite all the raging egos, bountiful volumes of data were published. And because there was a great deal of paper being shuffled around, cities were compelled by an altogether different doctrine of necessity to establish central statistical hubs. During the 1860s, statistical administrations were set up in Berlin, New York, Stockholm, Vienna, Rome, Leipzig, Frankfurt-am-Main, and many others. But from these central offices emerged a East/West statistics turf war, with France and England playing the role of Biggie on the West and Prussia as Tupac on the East. The West believed that a combination of individual competition and natural welfare best served society, while the East created the welfare state to solve these problems. And these attitudes, which Hacking is good enough to confess as caricaturish even as he illustrates a large and quite important point, affected the way in which statistics were perceived. If you believe in a welfare state, you’re probably not going to see laws forged from the printed numbers. Because numbers are all about individual action. And if you believe in the Hobbesian notion of free will, you’re going to look for statistical laws in the criminal numbers, because laws are formed by individuals. This created new notions of statistical fatalism. It’s worth observing that science at the time was also expected to account for morality.
Unusual experiments ensued. What, for example, could the chest circumference of a Scotsman tell us about the stability of the universe? (Yes, the measurement of Scottish chests was seriously considered by a Belgian guy named Adolphe Quetelet, who was trying to work out theories about the average man. When we get to Stephen Jay Gould’s The Mismeasure of Man several years from now, #21 in the Modern Library Nonfiction canon, I shall explore more pernicious measurement ideas promulgated as “science.” Stay tuned!) More nefariously, if you could chart the frequency of how often the working classes called in sick, perhaps you could establish laws to determine who was shirking duty, track the unruly elements, and punish the agitators interfering with the natural law. (As we saw with William Lamb Melbourne’s story, the British government was quite keen to crack down on trade unions during the 1830s. So just imagine what a rabid ideologue armed with a set of corrupted and unproven “laws” could do. In fact, we don’t even have to jump that far back in time. Aside from the obvious Hollerith punch card example, one need only observe the flawed radicalization model presently used by the FBI and the DHS to crack down on Muslim “extremists.” Arun Kundnani’s recent book, The Muslims Are Coming, examines this issue further. And a future Bat Segundo episode featuring Kundnani will discuss this dangerous approach at length.)
Throughout all these efforts to establish laws from numbers (Newton’s law of gravity had inspired a league of scientists to seek a value for this new G constant, a process that took more than a century), Charles Babbage, Johann Christian Poggendorf, and many others began publishing tables of constants. It is one thing to publish atomic weights. It is quite another to measure the height, weight, pulse, and breath of humans by gender and ethnicity (along with animals). The latter constant sets are clearly not as objective as Babbage would like to believe. And yet the universe does adhere to certain undeniable principles, especially when you have a large data set.
It took juries for mathematicians to understand how to reconcile large numbers with probability theory. In 1808, Pierre-Simon Laplace became extremely concerned with the French jury system. At the time, twelve-member juries convicted an accused citizen by a simple majority. He calculated that a seven-to-five majority had a chance of error of one in three. The French code had adopted the unusual method of creating a higher court of five judges to step in if there was a disagreement with a majority verdict in the lower court. In other words, if the majority of the judges in the higher court agreed with the minority of jurors in the lower court that an accused person should be acquitted, then the accused person would be acquitted. Well, this complicated system bothered Laplace. Accused men often faced execution in the French courts. So if there was a substantial chance of error, then the system needed to be reformed. Laplace began to consider juries composed of different sizes and verdicts ranging from total majority (12:0) to partial majority (9:3, 8:4), and he computed the following odds (which I have reproduced from a very helpful table in Hacking’s book):
The problems here become self-evident. You can’t have 1,001 people on a jury arguing over the fate of one man. On the other hand, you can’t have a 2/7 chance of error with a jury of twelve. (One of Laplace’s ideas was a 144 member jury delivering a 90:54 verdict. This involved a 1/773 chance of error. But that’s nowhere nearly as extreme as a Russian mathematician named M.V. Ostrogradsky, who wasted much ink arguing that a 212:200 majority was more reliable than a 12:0 verdict. Remember all this the next time you receive a jury duty notice. Had some of Laplace’s understandable concerns been more seriously considered, there’s a small chance that societies could have adopted larger juries in the interest of a fair trial.)
French law eventually changed the minimum conviction from 7:5 to 8:4. But it turned out that there was a better method to allow for a majority jury verdict. It was a principle that extended beyond mere frequency and juror reliability, taking into account Bernoulli’s ideas on drawing black and white balls from an urn to determine a probability value. It was called the law of large numbers. And the great thing is that you can observe this principle in action through a very simple experiment.
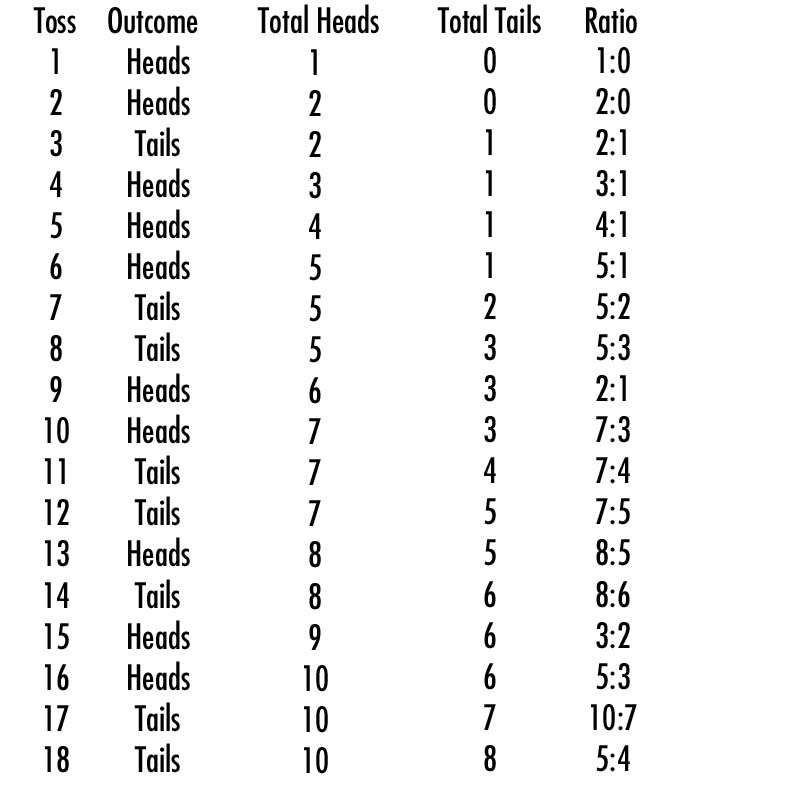
Here’s a way of seeing the law of large numbers in action. Take a quarter and flip it. Write down whether the results are heads or tails. Do it again. Keep doing this and keep a running tally of how many times the outcome is heads and how many times the coin comes up tails. For readers who are too lazy to try this at home, I’ve prepared a video and a table of my coin toss results:
The probability of a coin toss is 1:1. On average, the coin will turn up heads 50% of the time and tails 50% of the time. As you can see, while my early tosses leaned heavily towards heads, by the time I had reached the eighteenth toss, the law of large numbers ensured that my results skewed closer to 1:1 (in this case, 5:4) as I continued to toss the coin. Had I continued to toss the coin, I would have come closer to 1:1 with every toss.
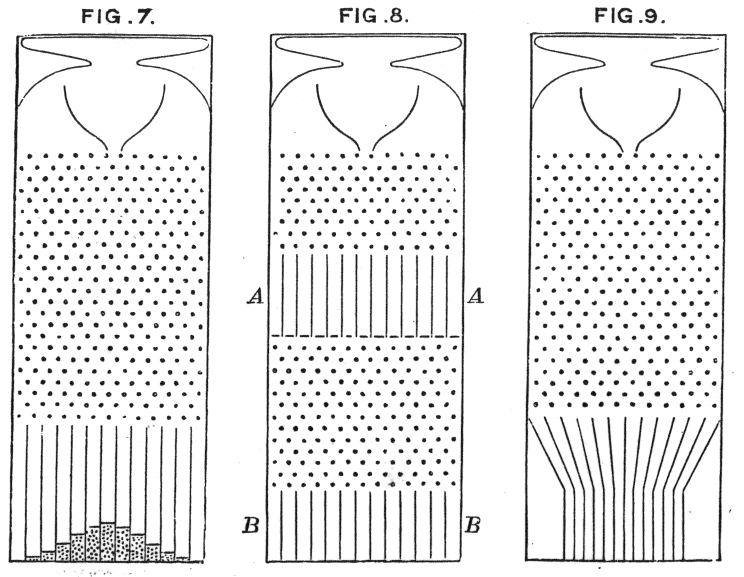
The law of large numbers offered the solution to Laplace’s predicament. It also accounts for the mysterious picture at the head of this essay. That image is a working replica of a Galton box (also known as a quincunx). (If you’re ever in Boston, go to the Museum of Science and you can see a very large working replica of a Galton box in action.) Sir Francis Galton needed a very visual method of showing off the central limit theorem. So he designed a box, not unlike a pachinko machine, in which beans are dropped from the top and work their way down through a series of wooden pins, which cause them to fall along a random path. Most of the beans land in the center. Drop more beans and you will see a natural bell curve form, illustrating the law of large numbers and the central limit theorem.
Despite all this, there was still the matter of statistical fatalism to iron out, along with an understandable distrust of statistics among artists and the general population, which went well beyond Disraeli’s infamous “There are three kinds of lies: lies, damned lies, and statistics” quote. Hacking is a rigorous enough scholar to reveal how Dickens, Dostoevsky, and Balzac were skeptical of utilitarian statistics. Balzac, in particular, delved into “conjugal statistics” in his Physiology of Marriage to deduce the number of virtuous women. They had every reason to be, given how heavily philosophers leaned on determinism. (See also William James’s “The Dilemma of Determinism.”) A German philosopher named Ernst Cassirer was a big determinism booster, pinpointing its beginnings in 1872. Hacking challenges Cassierer by pointing out that determinism incorporated the doctrine of necessity earlier in the 1850s, an important distinction in returning back to Peirce’s idea of absolute chance.
I’ve been forced to elide a number of vital contributors to probability and some French investigations into suicide in an attempt to convey Hacking’s intricate narrative. But the one word that made Perice’s contributions so necessary was “normality.” This was the true danger of statistical ideas being applied to the moral sciences. When “normality” became the ideal, it was greatly desirable to extirpate anything “abnormal” or “aberrant” from the grand human garden, even though certain crime rates were indeed quite normal. We see similar zero tolerance measures practiced today by certain regressive members of law enforcement or, more recently, New York Mayor Bill de Blasio’s impossible pledge to rid New York City of all traffic deaths by 2024. As the law of large numbers and Galton’s box observed, some statistics are inevitable. Yet it was also important for Peirce to deny the doctrine of necessity. Again, without chance, Peirce pointed out that we could not have had all these laws in the first place.
It was strangely comforting to learn that, despite all the nineteenth century innovations in mathematics and probability, chance remains very much a part of life. Yet when one begins to consider stock market algorithms (and the concomitant flash crashes), as well as our collective willingness to impart voluminous personal data to social media companies who are sharing these numbers with other data brokers, I cannot help but ponder whether we are willfully submitting to another “law of large numbers.” Chance may favor the prepared mind, as Pasteur once said. So why court predictability?
* Peirce’s attempts to secure academic employment and financial succor were thwarted by a Canadian scientist named Simon Newcomb. (A good overview of the correspondence between the two men can be found at the immensely helpful “Perice Gateway” website.)


This is wonderful, informative- and timely (the internet!) Also, I was mildly obsessed with Gould and the idea of punctuated equilibrium- which comes up in my stories from time to time. I look forward to you reading and writing about him.